Om du arbetar med en triangel med en rät vinkel i någonstans, är det enkelt att hitta tangentvinkeln, så länge du vet längden på två sidor av triangeln.
Att göra det är ännu enklare i Microsoft Excel eftersom det finns inbyggda funktioner som du kan använda.
Informationen i den här artikeln gäller Excel för Microsoft 365, Excel 2019, 2016, 2013, 2010 och Excel för Mac.
What is the Tangent Angle?
En tangentvinkel är en vinkel i triangeln där du vet längden på sidan mitt emot vinkeln och sidan intill den.
Föreställ dig till exempel att din chef säger åt dig att justera en stege på exakt 70 grader från marken. Om du inte har några specialverktyg skulle det vara komplicerat att mäta om vinkeln mellan stegen och marken är exakt 70 grader.
Men om du har ett måttband kan du mäta avståndet från botten av stegen till väggen. Eftersom stegen mot väggen bildar en triangel, skulle detta vara den sida som är intill till tangentvinkeln du försöker beräkna.
Närnäst skulle du mäta avståndet från botten av väggen till där toppen av stegen vidrör den. Detta är avståndet för sidan som är motsatt från tangentvinkeln.
Med mätning av de motsatta och intilliggande sidorna kan du beräkna vinkeln vid stegens bas med hjälp av arctangent-funktionen.
Om väggens (motsatta) sida är 10 fot och marksidan (intilliggande) är 5 fot, är formeln för tangentvinkeln den motsatta sidan dividerad med den intilliggande sidan. Detta är 10 dividerat med 5, eller 0,5.
För att hitta värdet för vinkeln måste du ta arctangenten på 0,5.
Hitta tangensvinkeln med Excel
Du kan hitta en kalkylator som beräknar arctangensen för ett värde, men Excel har en inbyggd funktion som heter ATAN som du kan använda.
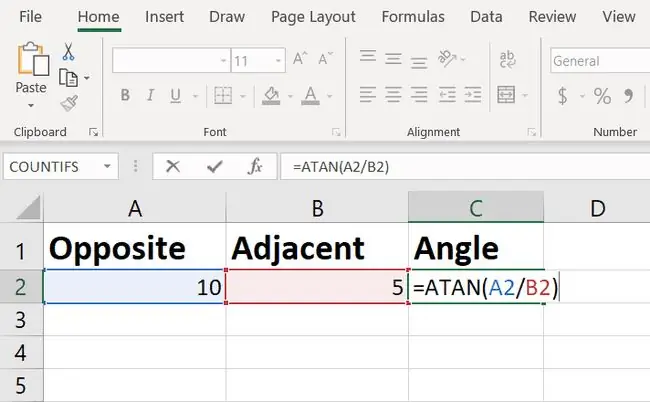
Formeln returnerar vinkeln i radianer, vilket din chef förmodligen inte kommer att förstå.
Du vill konvertera radianer till grader genom att multiplicera det med 180/pi. Excel har också en PI-funktion som du kan använda för detta ändamål.
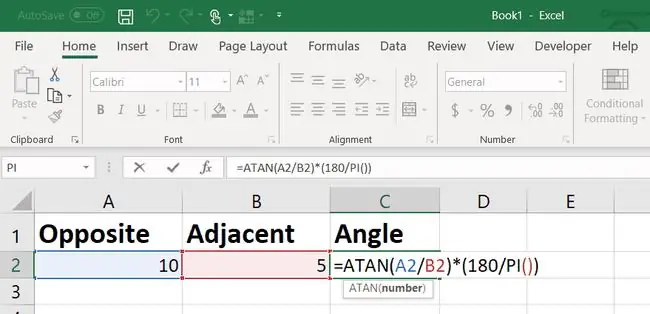
Svaret, i det här fallet, är 63,43 grader. Det betyder att du måste justera en av längderna tills vinkeln är exakt 70 grader.
Det är enkelt att göra detta i Excel eftersom du kan ändra värdet på den motsatta sidan tills arctangensresultatet är 70.
Använda ASIN och ACOS i Excel
I samma scenario, låt oss säga att du inte har ett måttband som är tillräckligt länge för att mäta väggen. Du vet bara att stegen är 15 fot och att den är placerad fem fot från väggen.
Excel har två andra funktioner som du kan använda för att beräkna vinkeln.
Stegens längd är hypotenuse för triangeln, och markavståndet är intilliggande sidan till vinkeln. Så länge triangeln har en rät (90 grader) vinkel, bestämmer informationen du har vilken formel du behöver använda.
- Cosinus: Beräkna cosinusvinkeln om du vet längden på hypotenusan och den intilliggande sidan.
- sinus: Beräkna sinusvinkeln om du vet längden på hypotenusan och den motsatta sidan.
I det här fallet är vinkeln arccosinus för den intilliggande sidan dividerat med hypotenusan.
Eftersom du vet att den intilliggande sidan (markavståndet) är 5 fot, och stegens längd (hypotenus) är 15 fot, är cosinus för vinkeln 5 dividerat med 15, eller 0,333.
För att beräkna vinkeln, använd arccosinusformeln i Excel.
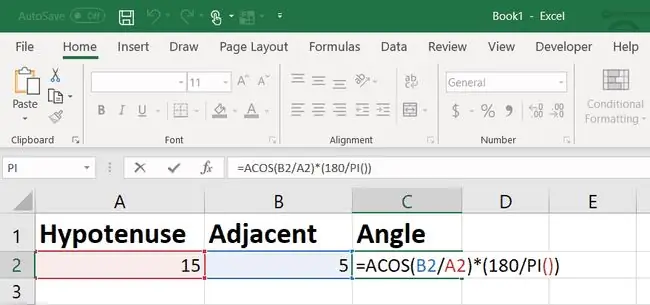
Resultatet av arccosine-funktionen är att Excel är i radianer, så du måste multiplicera det med 180/PI för att omvandla det till grader.
För en 15 fot stege med basen 5 fot från väggen är vinkeln 70,53 grader.
Om du visste att höjden på väggen (den motsatta sidan) är 10 fot, istället för markavståndet från väggen (den intilliggande sidan), skulle du använda bågformeln i Excel.
I det här fallet är vinkelns sinus den motsatta sidan dividerat med hypotenusan.
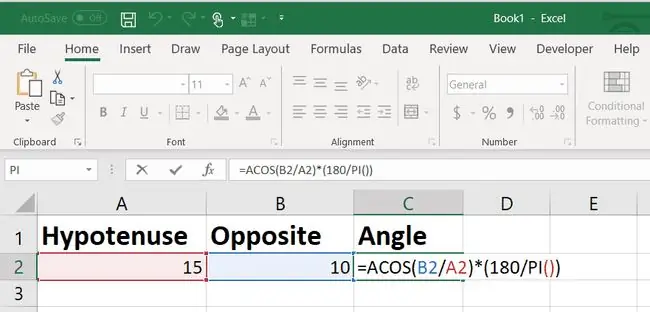
Efter omvandling till grader skulle vinkeln, i det här fallet, vara 48,12 grader.
Varför använda ATAN, ACOS eller ASIN?
Här är några exempel på situationer där du kan behöva använda någon av dessa funktioner i Excel:
- Inom snickeri och konstruktion används vinklar och längder i alla aspekter av att bygga hus och byggnader.
- Fotografer använder vinklar för att anpassa belysningen och sina kreativa bilder noggrant.
- I sport kan förståelsevinklar förbättra färdigheter och förbättra strategi.
- Fartyg och flygplan finns på radar med hjälp av vinklar och avstånd.
- Om du vill vara säker på att möbler passar rätt i ditt rum måste du veta hur du beräknar längder och vinklar.
Du kanske kan utföra dessa beräkningar på en vetenskaplig miniräknare. Men om du inte har en till hands kan Excel hjälpa dig att göra dessa beräkningar.
